2. Introduction¶
The Vector Boolean Function Library (VBF) is a collection of C++ classes designed for analyzing Vector Boolean Functions (functions that map a Boolean vector to another Boolean vector) from a cryptographic perspective. This implementation uses the NTL library from Victor Shoup, modifying some of the general purpose modules of this library (to make it better suited to cryptography), and adding new modules that complement the existing ones. The class representing a Vector Boolean Function can be initialized by several data structures such as Truth Table, Trace representation, Algebraic Normal Form (ANF) among others. The most relevant cryptographic criteria for both block and stream ciphers can be evaluated with VBF. It allows to obtain some interesting cryptologic characterizing features such as linear structures, frequency distribution of the absolute values of the Walsh Spectrum or Autocorrelation Spectrum, among others. In addition, operations such as equality checking, composition, inversion, sum, direct sum, concatenation, bricklayering (parallel application of Vector Boolean Functions as employed in Rijndael cipher), and adding coordinate functions of two Vector Boolean Functions can be executed.
2.1. Functions available in VBF¶
The library covers a wide range of topics for analyzing cryptographic properties of Vector Boolean Functions. Methods are available for the following areas:
- Vector Boolean Function representations and characterizations
- Cryptographic criteria calculation
- Constructions and operations over Vector Boolean functions
The use of these methods is described in this manual. Each chapter provides detailed definitions of the methods, followed by example programs.
2.2. Conventions used in this manual¶
This manual contains many examples which can be typed at the keyboard. A command entered at the terminal is shown like this,
$ command
The first character on the line is the terminal prompt, and should not be typed. The dollar sign $ is used as the standard prompt in this manual, although some systems may use a different character.
The examples assume the use of the GNU operating system. There may be minor differences in the output on other systems. The commands for setting environment variables use the Bourne shell syntax of the standard GNU shell (bash).
2.3. Software implementation¶
The package included consists of:
- Derived classes inherited from NTL base classes which add new functions on top of them:
pol.h, vbf_GF2EX.h, vbf_GF2X.h, vbf_ZZ.h, vbf_mat_GF2.h, vbf_mat_RR.h, vbf_mat_ZZ.h, vbf_tools.h,
vbf_vec_GF2.h, vbf_vec_GF2E.h, vbf_vec_RR.h, vbf_vec_ZZ.h, vec_pol.h
- Main class (VBF.h) with the functions and other .h files,
- A makefile to ease the compilation of example (Makefile),
- A set of files associated with the decimal representation of KASUMI [KASUMI:05] S-boxes (S7.dec and S9.dec).
The Output files can be found within “KASUMI Analysis” in the “Analysis of other cryptographic algorithms” menu at `http://vbf.rtfd.io`_.
2.4. System requirements¶
The VBF library can be easily installed in a matter of minutes on just about any platform, including virtually any 32- or 64-bit machine running any flavor of Unix, as well as PCs running Windows, and Macintoshes. VBF achieves this portability by avoiding esoteric C++ features, and by avoiding assembly code; it should therefore remain usable for years to come with little or no maintenance, even as processors and operating systems continue to change and evolve.
2.5. Installation¶
We are going to illustrate the installation of the package in an Unix or Unix-like platforms (including Linux distributions).
- Download the lastest version of the library from VBF source code URL and place it in the working directory. You should see the example program, input files and the “*.h” files.
- Obtain NTL library source code. To obtain the source code and documentation for NTL, download ntl-xxx.tar.gz from Download NTL library, placing it in a different directory.
- Run the configuration script. Working in the directory where you placed the NTL library, do the following (here, “xxx” denotes the desired version number of NTL; any version of NTL can be employed):
$ cd ntl-xxx/src
$ ./configure
The execution of configure generates the file “makefile” and the file “../include/NTL/config.h”, based upon the values assigned to the variables on the command line. In the example above no arguments were employed. The most important variables are: “CC” for choosing the C compiler, “CXX” for choosing the C++ compiler, “PREFIX” for choosing the directory in which to install NTL library components.
Disable GMP
If you really do not want to use GMP, you can pass the option NTL_GMP_LIP=off to configure. More information on A Tour of NTL: Obtaining and Installing NTL for UNIX
- Build NTL:
$ make
$ make check
$ make install
The make execution in the directory src/ compiles all the source files and creates a library ntl.a in the same directory. Some testing programs are run by means of the command make check. Lastly, make install performs among other actions the copy of the library file ntl.a into /usr/local/lib/libntl.a by default. It is not necessary to execute make check in each NTL building as it takes a long time. In order to execute make install, it is necessary to have privileged user permissions as some directories creation, file deletion, changes of file attributes, and copies of files are done.
Do not forget to use an account with appropriate permissions: root for instance.
2.6. Preliminaries¶
The mathematical theory of Vector Boolean Functions starts with the formal definition of vector spaces whose elements (vectors) have binary elements. Let 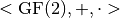 be the finite field of order 2, where
be the finite field of order 2, where 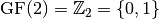 ,
, 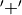 the ‘integer addition modulo 2’ and
the ‘integer addition modulo 2’ and 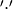 the ‘integer multiplication modulo 2’.
the ‘integer multiplication modulo 2’. 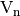 is the vector space of n-tuples of elements from
is the vector space of n-tuples of elements from 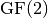 . The direct sum of
. The direct sum of 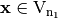 and
and 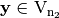 is defined as
is defined as 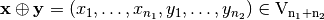 . The inner product of
. The inner product of 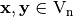 is denoted by
is denoted by  , and the inner product of real vectors
, and the inner product of real vectors 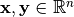 is denoted by
is denoted by 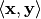 .
.
One can now define binary functions between this type of vector spaces, whose linearity analysis (for robustness-against-attacks purposes) will become very important. 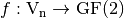 is called a Boolean function and
is called a Boolean function and 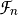 is the set of all Boolean functions on
is the set of all Boolean functions on 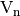 .
. 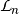 is the set of all linear Boolean functions on
is the set of all linear Boolean functions on 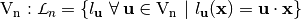 and
and 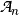 is the set of all affine Boolean functions
on
is the set of all affine Boolean functions
on 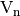 .
.
It is possible to characterize Boolean functions via alternative and very useful associated mappings. In the following, some of these mappings are presented. The real-valued mapping 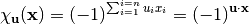 for
for 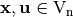 is called a character. The character form of
is called a character. The character form of 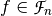 is defined as
is defined as 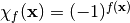 . The Truth Table of
. The Truth Table of 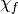 is called as the (1,-1)-sequence vector or sequence vector of
is called as the (1,-1)-sequence vector or sequence vector of 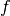 and is denoted by
and is denoted by 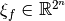 .
.
Let 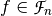 be a Boolean function; the Walsh Transform of
be a Boolean function; the Walsh Transform of 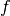 at
at 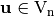 is the n-dimensional Discrete Fourier Transform and can be calculated as follows:
is the n-dimensional Discrete Fourier Transform and can be calculated as follows:
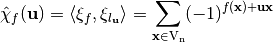
The autocorrelation of 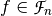 with respect to the shift
with respect to the shift 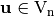 is a measure of the statistical dependency among the involved variables (indicating robustness against randomness-based attacks). It is the cross-correlation of
is a measure of the statistical dependency among the involved variables (indicating robustness against randomness-based attacks). It is the cross-correlation of 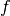 with itself, denoted by
with itself, denoted by 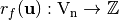 and defined by [1]:
and defined by [1]:
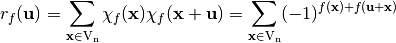
The directional derivative of 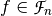 in the direction of
in the direction of 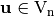 is defined by:
is defined by:
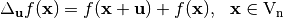
We shall call the linear kernel of 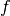 the set of those vectors
the set of those vectors 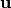 such that
such that 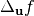 is a constant function. The linear kernel of any Boolean function is a subspace of
is a constant function. The linear kernel of any Boolean function is a subspace of 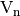 . Any element
. Any element 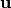 of the linear kernel of
of the linear kernel of 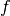 is said to be a linear structure of
is said to be a linear structure of 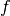 .
.
Given 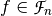 , a nonzero function
, a nonzero function 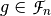 is called an annihilator of
is called an annihilator of 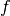 if
if 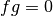 .
.
We now extend the scope of the study by considering functions between any pair of binary-valued vector spaces. 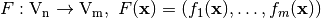 is called a Vector Boolean function and
is called a Vector Boolean function and 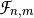 is the set of all Vector Boolean Functions
is the set of all Vector Boolean Functions 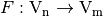 . Each
. Each 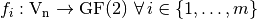 is a coordinate function of
is a coordinate function of 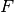 . The indicator function of
. The indicator function of  , denoted by
, denoted by 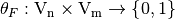 , is defined in [ChabaudV:94] as:
, is defined in [ChabaudV:94] as:
(1)¶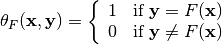
Again, several mappings associated with a Vector Boolean Functions can be defined, in similar terms to the binary functions case. Hence, the character form of 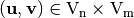 can be defined as follows:
can be defined as follows: 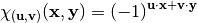 . Similarly, let
. Similarly, let  be a Vector Boolean function; its Walsh Transform is the two-dimensional Walsh Transform defined by:
be a Vector Boolean function; its Walsh Transform is the two-dimensional Walsh Transform defined by:
(2)¶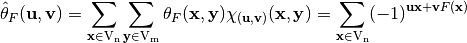
Also, the autocorrelation of  with respect to the shift
with respect to the shift 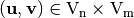 is the cross-correlation of
is the cross-correlation of 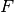 with itself, denoted by
with itself, denoted by 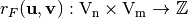 , so that [fse-Nyberg:94]:
, so that [fse-Nyberg:94]:
(3)¶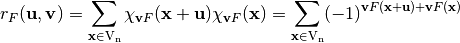
Let 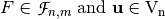 , then the difference Vector Boolean function of
, then the difference Vector Boolean function of 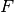 in the direction of
in the direction of 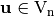 , denoted by
, denoted by 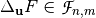 is defined as follows:
is defined as follows: 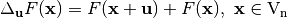 . If the following equality is satisfied:
. If the following equality is satisfied:
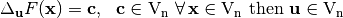 is called a linear structure of
is called a linear structure of 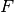 .
.
Finally, we define the simplifying notation for the maximum of the absolute values of a set of real numbers 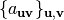 , characterized by vectors
, characterized by vectors 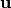 and
and 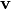 , as:
, as:  . Using the same simplifying notation, we can define the
. Using the same simplifying notation, we can define the 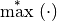 operator on a set of real numbers
operator on a set of real numbers 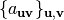 , as:
, as: 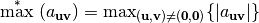 . This notation will be used in some criteria definitions.
. This notation will be used in some criteria definitions.
Footnotes
| [1] | Most authors omit the factor 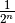 |
2.7. Design Philosophy¶
The core of VBF library is the VBF class which represents Vector Boolean Functions whose data members and member functions make use of the NTL modules listed in Table NTL Modules. However, some new cryptography-related member functions were added to the previous modules. Besides, new modules which are not present in NTL, are defined and they are listed in Table New Modules.
| NTL modules used in VBF | |
|---|---|
| CLASS NAME | DESCRIPTION |
GF2 |
Galois Field of order 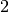 denoted by denoted by 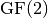 |
vec_GF2 |
Vectors over 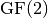 |
mat_GF2 |
Matrices over 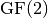 |
RR |
Arbitrary-precision floating point numbers |
vec_RR |
Vectors over reals |
mat_RR |
Matrices over reals |
ZZ |
Signed, arbitrary length integers |
vec_ZZ |
Vectors over integers |
mat_ZZ |
Matrices over integers |
GF2X |
Implements polynomial arithmetic modulo 2 |
GF2E |
Polynomials in ![F_2[X]](_images/math/3e066d881655b61b961177145f13c93108ae2891.png) modulo a polynomial modulo a polynomial 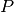 |
GF2EX |
Polynomials over 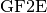 |
vec_GF2E |
Vectors over 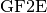 |
Note that the modulus P in 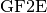 may be any polynomial with degree greater than 0, not necessarily irreducible. Objects of the class
may be any polynomial with degree greater than 0, not necessarily irreducible. Objects of the class 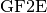 are represented as a
are represented as a 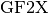 of degree less than the degree of P.
of degree less than the degree of P. 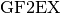 can be used, for example, for arithmetic in
can be used, for example, for arithmetic in ![\gf{GF(2^n)[X]}](_images/math/4f8dc01fafd4ced4fbc7d4e28f8246c79d39ae24.png) .
.
| New modules created for VBF | |
|---|---|
| CLASS NAME | DESCRIPTION |
pol |
Polynomial in ANF of a Boolean Function |
vec_pol |
Polynomials in ANF of a Vector Boolean Function |
The main file in the library, called VBF.h has the definitions of the objects described in the next chapters.