7. Analysis of AES competition cryptographic algorithms¶
In January 1997, the US National Institute of Standards and Technology (NIST) announced the start of an initiative to develop a new encryption standard: the AES. The AES selection process was open in which 15 candidates were accepted for the first evaluation round and 5 finalists were announced in the second round. On October 2, 2000, NIST officially announced that Rijndael would become the AES. In this chapter, a number of cryptographic algorithms from the AES (Advanced Encryption Standard) candidates accepted for the first evaluation round process are analysed.
Below you can find a legend describing the cryptographic criteria used in this chapter:
| NL | Nonlinearity |
| NL2 | 2-nd order nonlinearity |
| LD | Linearity distance |
| DEG | Algebraic degree |
| AI | Algebraic immunity |
| MAXAC | Absolute indicator |
 |
Sum-of-squares indicator |
| LP | Linear potential |
| DP | Differential Potential |
Hyperlinks to representations
Open the hyperlinks to representations below in a new browser window or in a new tab.
7.1. CAST-256¶
7.1.1. Description¶
CAST-256 is a symmetric-key block cipher published in June 1998. It was submitted as a candidate for the Advanced Encryption Standard (AES); however, it was not among the five AES finalists. It is an extension of an earlier cipher, CAST-128; both were designed according to the “CAST” design methodology invented by Carlisle Adams and Stafford Tavares. Howard Heys and Michael Wiener also contributed to the design. It has four 8x32 S-boxes: S1,S2,S3 and S4.
7.2. Crypton¶
7.2.1. Description¶
CRYPTON is a symmetric block cipher designed by Chae Hoon Lim of Future Systems Inc. In this section, we study both the AES proposal (v0.5) and the revised version (v1.0). In v0.5 the authors used two 8x8 S-boxes constructed from 4-bit permutations using a 3-round Feistel Cipher (Tabular representation of S-boxes). In v1.0 the authors used four variants of one S-box, instead of independent four S-boxes to allow greater flexibility in memory requirements. The four 8x8 S-boxes are 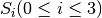 , such that
, such that 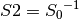 and
and 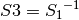
7.2.2. Summary¶
| S-box | NL | LD | DEG | AI | MAXAC |  |
LP | DP |
|---|---|---|---|---|---|---|---|---|
| S0 (v0.5) | 96 | 32 | 5 | 3 | 128 | 581632 | 0.0625 | 0.03125 |
| S1 (v0.5) | 96 | 28 | 5 | 3 | 144 | 581632 | 0.0625 | 0.03125 |
| S0 (v1.0) | 96 | 40 | 6 | 4 | 96 | 280192 | 0.0625 | 0.0390625 |
| S1 (v1.0) | 96 | 40 | 6 | 4 | 96 | 280192 | 0.0625 | 0.0390625 |
| S2 (v1.0) | 96 | 40 | 6 | 4 | 96 | 280192 | 0.0625 | 0.0390625 |
| S3 (v1.0) | 96 | 40 | 6 | 4 | 96 | 280192 | 0.0625 | 0.0390625 |
7.2.3. S0 (v0.5)¶
7.2.3.1. Representations¶
Polynomial representation in ANF
Walsh Spectrum representation (except first row and column):
7.2.3.2. Other useful information in cryptanalysis¶
Cycle structure:
| Cycle length | Number of cycles |
|---|---|
| 1 | 1 |
| 3 | 1 |
| 7 | 3 |
| 10 | 2 |
| 11 | 2 |
| 15 | 1 |
| 16 | 2 |
| 17 | 1 |
| 22 | 1 |
| 42 | 1 |
| 61 | 1 |
There are no linear structures
It has 1 fixed point: (0,0,0,0,1,1,1,1)
It has 1 negated fixed point: (1,1,1,0,1,1,1,1)
7.2.4. S1 (v0.5)¶
7.2.4.1. Representations¶
Polynomial representation in ANF
Walsh Spectrum representation (except first row and column):
7.2.4.2. Other useful information in cryptanalysis¶
Cycle structure:
| Cycle length | Number of cycles |
|---|---|
| 1 | 1 |
| 3 | 1 |
| 7 | 3 |
| 10 | 2 |
| 11 | 2 |
| 15 | 1 |
| 16 | 2 |
| 17 | 1 |
| 22 | 1 |
| 42 | 1 |
| 61 | 1 |
There are no linear structures
It has 1 fixed point: (0,0,0,0,1,1,1,1)
It has 1 negated fixed point: (0,0,0,1,0,0,0,0)
7.2.5. S0 (v1.0)¶
7.2.5.1. Representations¶
Polynomial representation in ANF
Walsh Spectrum representation (except first row and column):
7.2.5.2. Other useful information in cryptanalysis¶
Cycle structure:
| Cycle length | Number of cycles |
|---|---|
| 1 | 1 |
| 2 | 1 |
| 5 | 1 |
| 248 | 1 |
There are no linear structures
It has 1 fixed point: (0,1,1,1,0,1,0,1)
It has no negated fixed points
7.2.6. S1 (v1.0)¶
7.2.6.1. Representations¶
Polynomial representation in ANF
Walsh Spectrum representation (except first row and column):
7.2.6.2. Other useful information in cryptanalysis¶
Cycle structure:
| Cycle length | Number of cycles |
|---|---|
| 3 | 1 |
| 5 | 1 |
| 12 | 1 |
| 22 | 1 |
| 28 | 1 |
| 48 | 1 |
| 50 | 1 |
| 88 | 1 |
There are no linear structures
It has no fixed points
It has 1 negated fixed point: (1,0,1,0,1,1,1,0)
7.2.7. S2 (v1.0)¶
7.2.7.1. Representations¶
Polynomial representation in ANF
Walsh Spectrum representation (except first row and column):
7.2.7.2. Other useful information in cryptanalysis¶
Cycle structure:
| Cycle length | Number of cycles |
|---|---|
| 1 | 1 |
| 2 | 1 |
| 5 | 1 |
| 248 | 1 |
There are no linear structures
It has 1 fixed point: (0,1,1,1,0,1,0,1)
It has no negated fixed points
7.2.8. S3 (v1.0)¶
7.2.8.1. Representations¶
Polynomial representation in ANF
Walsh Spectrum representation (except first row and column):
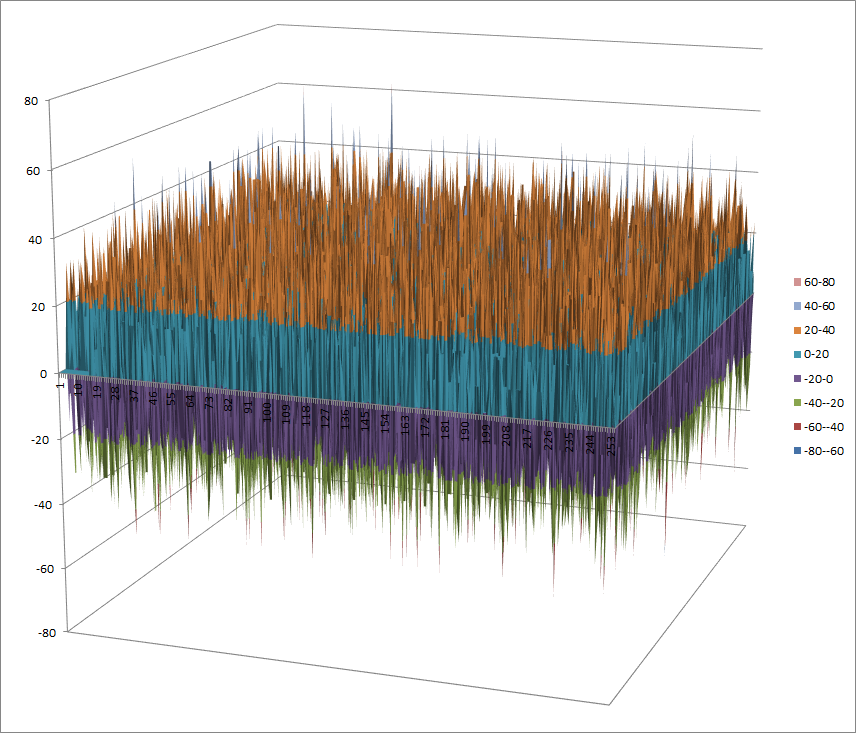
7.2.8.2. Other useful information in cryptanalysis¶
Cycle structure:
| Cycle length | Number of cycles |
|---|---|
| 3 | 1 |
| 5 | 1 |
| 12 | 1 |
| 22 | 1 |
| 28 | 1 |
| 48 | 1 |
| 50 | 1 |
| 88 | 1 |
There are no linear structures
It has no fixed points
It has 1 negated fixed point: (0,1,0,1,0,0,0,1)
7.3. DEAL¶
7.3.1. Description¶
DEAL (Data Encryption Algorithm with Larger blocks) is a symmetric block cipher derived from the Data Encryption Standard (DES). The design was proposed in a report by Lars Knudsen in 1998, and was submitted to the AES competition by Richard Outerbridge (who notes that Knudsen had presented the design at the SAC conference in 1997).
DEAL has eight 6x4 S-boxes: S1, S2, S3, S4, S5, S6, S7, S8. They are the same as DES S-boxes and you can see an analysis in DES.
7.4. E2¶
7.4.1. Description¶
E2 is a symmetric block cipher which was created in 1998 by NTT and submitted to the AES competition. E2 has an input transformation and output transformation that both use modular multiplication, but the round function itself consists only of XORs and S-box lookups. The single 8×8-bit S-box is constructed from the composition of an affine transformation with the discrete exponentiation 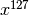 over the finite field
over the finite field 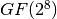 . NTT adopted many of E2’s special characteristics in Camellia, which has essentially replaced E2.
. NTT adopted many of E2’s special characteristics in Camellia, which has essentially replaced E2.
7.4.2. Summary¶
| S-box | NL | LD | DEG | AI | MAXAC |  |
LP | DP |
|---|---|---|---|---|---|---|---|---|
| S | 100 | 38 | 6 | 4 | 104 | 236800 | 0.0478515625 | 0.0390625 |
7.4.3. S¶
7.4.3.1. Representations¶
Polynomial representation in ANF
Walsh Spectrum representation (except first row and column):
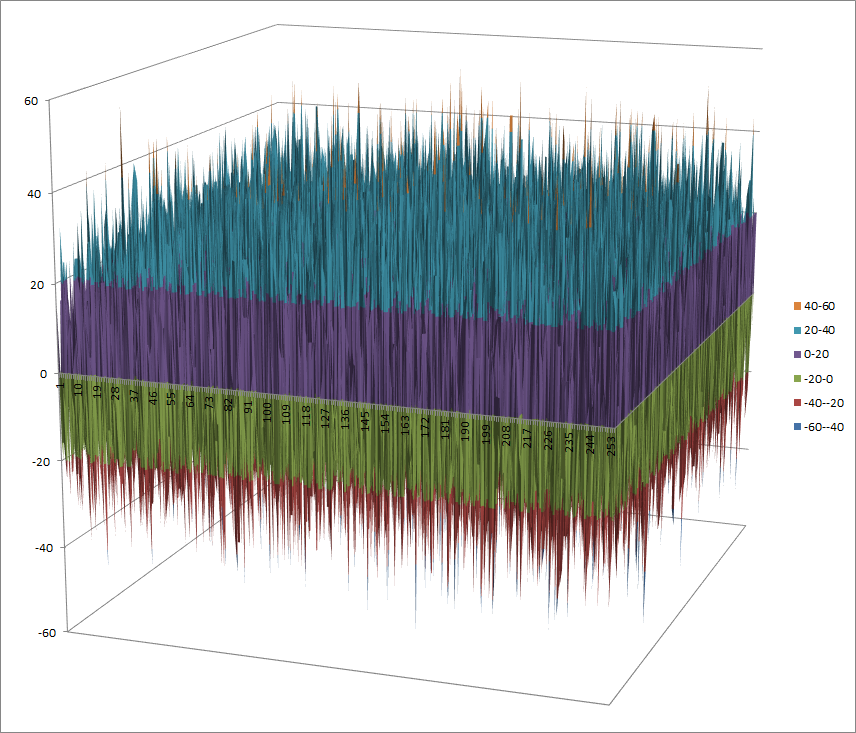
7.4.3.2. Other useful information in cryptanalysis¶
Cycle structure:
| Cycle length | Number of cycles |
|---|---|
| 2 | 1 |
| 3 | 1 |
| 7 | 1 |
| 24 | 1 |
| 64 | 1 |
| 156 | 1 |
There are no linear structures
It has no fixed points.
It has 2 negated fixed points: (0,0,1,0,1,0,0,1), (1,0,0,0,1,0,1,1)
7.5. LOKI97¶
7.5.1. Description¶
LOKI97 is a block cipher which was a candidate in the Advanced Encryption Standard competition. It is a member of the LOKI family of ciphers, earlier instances being LOKI89 and LOKI91. LOKI97 was designed by Lawrie Brown, assisted by Jennifer Seberry and Josef Pieprzyk. The LOKI97 round function uses two columns each with multiple copies of two basic S-boxes. The S-boxes chosen for LOKI97 use cubing in a galois field 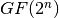 with n odd. In order to use odd sized inputs, S1 uses 13 input bits, and S2 uses 11. The S-box functions are:
with n odd. In order to use odd sized inputs, S1 uses 13 input bits, and S2 uses 11. The S-box functions are:
S1[x]=((x XOR 1FFF)^3 mod 2911) & FF 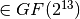
S2[x]=((x XOR 7FF)^3 mod AA7) & FF 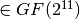
where all constant above are written in hex and all computations are done as polynomials in 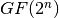 .
.
7.5.2. Summary¶
| S-box | size | NL | LD | DEG | AI | MAXAC |  |
LP | DP |
|---|---|---|---|---|---|---|---|---|---|
| S1 | 13x8 | 4032 | 0 | 2 | 2 | 8192 | 134217728 | 0.000244140625 | 0.0078125 |
| S2 | 11x8 | 992 | 0 | 2 | 2 | 2048 | 8388608 | 0.0009765625 | 0.0078125 |
7.5.3. S1¶
7.5.3.1. Representations¶
Polynomial representation in ANF
Walsh Spectrum representation (256x256 first values except first row and column):
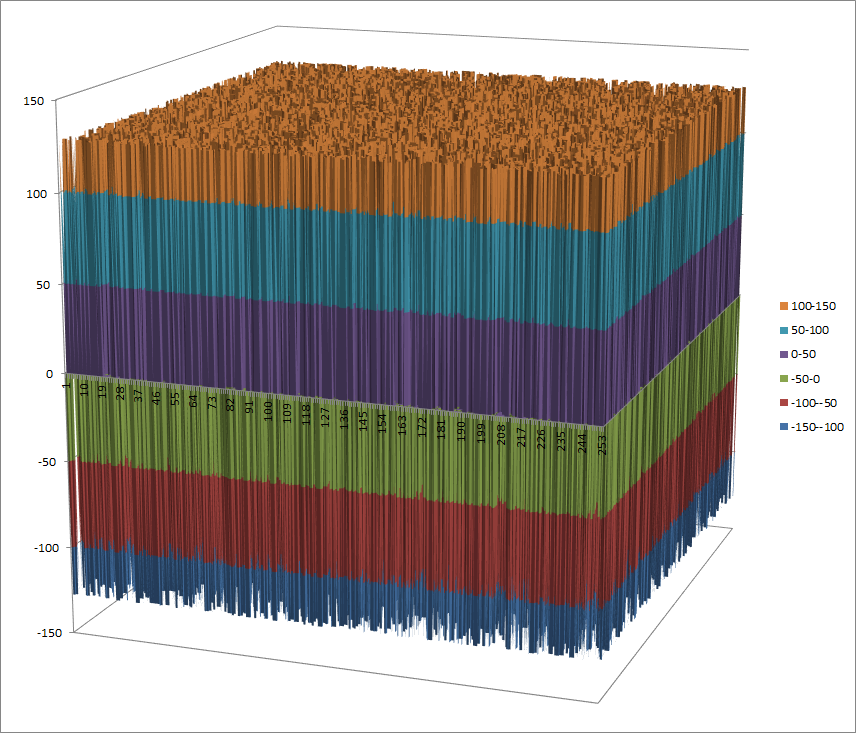
7.5.3.2. Other useful information in cryptanalysis¶
There are 255 linear structures:
7.5.4. S2¶
7.5.4.1. Representations¶
Polynomial representation in ANF
Walsh Spectrum representation (256x256 first values except first row and column):
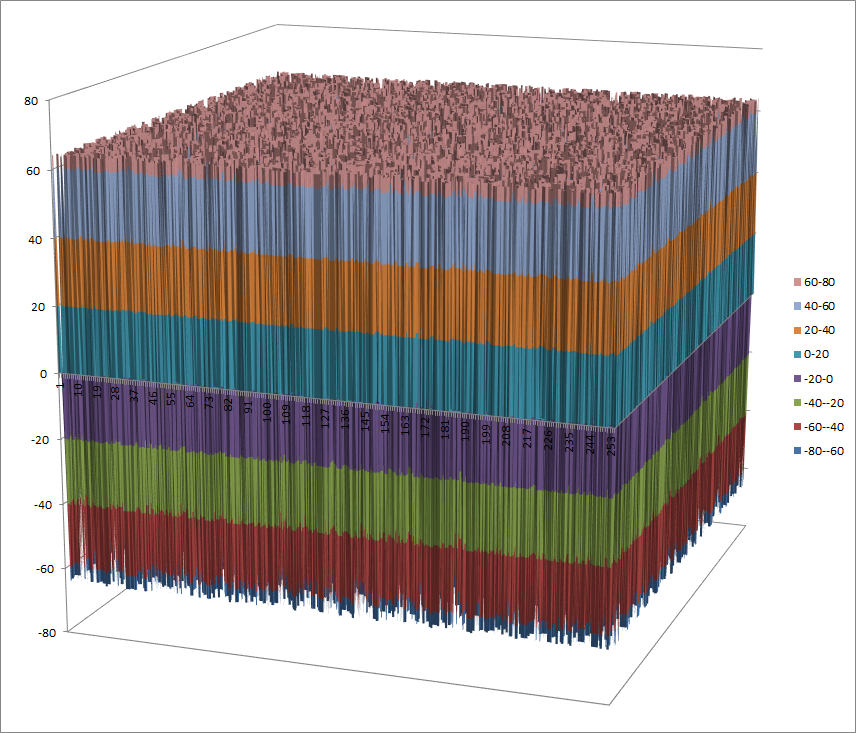
7.5.4.2. Other useful information in cryptanalysis¶
There are 256 linear structures:
7.6. Magenta¶
7.6.1. Description¶
Magenta is a symmetric key block cipher developed by Michael Jacobson Jr. and Klaus Huber for Deutsche Telekom. The cipher was submitted to the Advanced Encryption Standard process, but did not advance beyond the first round; cryptographic weaknesses were discovered and it was found to be one of the slower ciphers submitted. It has one 8x8 S-box.
7.6.2. Summary¶
| S-box | NL | LD | DEG | AI | MAXAC |  |
LP | DP |
|---|---|---|---|---|---|---|---|---|
| S | 102 | 44 | 7 | 4 | 80 | 217600 | 0.04125976563 | 0.03125 |
7.6.3. S¶
7.6.3.1. Representations¶
Polynomial function over 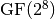 with irreducible polynomial
with irreducible polynomial 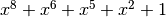 : Trace representation
: Trace representation
Polynomial representation in ANF
Walsh Spectrum representation (except first row and column):
7.6.3.2. Other useful information in cryptanalysis¶
Cycle structure:
| Cycle length | Number of cycles |
|---|---|
| 1 | 1 |
| 5 | 2 |
| 9 | 1 |
| 38 | 1 |
| 198 | 1 |
There are no linear structures
It has 1 fixed point: (1,0,1,0,0,0,0,1)
It has 2 negated fixed points: (0,0,0,1,1,1,0,0), (1,1,1,1,1,1,1,1)
7.7. Mars¶
7.7.1. Description¶
Mars is a block cipher that was IBM’s submission to the Advanced Encryption Standard process. MARS was selected as an AES finalist in August 1999, after the AES2 conference in March 1999, where it was voted as the fifth and last finalist algorithm. It has two 8x32 S-boxes: S0 and S1
7.8. Rijndael¶
7.8.1. Description¶
Rijndael, later called AES, is a block cipher used for securing sensitive but unclassified material by U.S. Government agencies since December 6, 2001 and has become the de facto encryption standard for commercial transactions in the private sector.
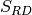 is AES 8x8 S-box and it is generated by determining the multiplicative inverse for a given number in
is AES 8x8 S-box and it is generated by determining the multiplicative inverse for a given number in ![GF(2^8) = GF(2)[x]/(x^8 + x^4 + x^3 + x + 1)](_images/math/9b0c03982470bb4f3bf5cb5ef6379a3af6b4d358.png) , Rijndael’s finite field.
, Rijndael’s finite field. 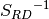 is the inverse S-box and it is simply the S-box
is the inverse S-box and it is simply the S-box 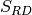 run in reverse.
run in reverse.
The tabular representation of 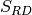 S-box represented in hexadecimal notation is the following:
S-box represented in hexadecimal notation is the following:
Tabular representation in hexadecimal notation
Here the column is determined by the least significant nibble (four-bit aggregation), and the row is determined by the most significant nibble. For example, the value 0x9a is converted into 0xb8 by Rijndael’s S-box. Note that the multiplicative inverse of 0x00 is defined as itself.
The tabular representation of 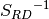 S-box represented in hexadecimal notation is the following:
S-box represented in hexadecimal notation is the following:
Tabular representation in hexadecimal notation
For hardware implementations, it might be useful to use the following decomposition of 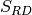 :
:
![S_{RD}[a] = f(g(a))](_images/math/b840bab3cc091494164d1d61a233b96cfa110643.png)
where 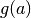 is the mapping
is the mapping
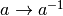 in
in 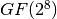 , and
, and 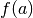 is an affine mapping. Since
is an affine mapping. Since 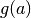 is self-inverse, we have:
is self-inverse, we have:
![{S_{RD}}^{-1}[a] = {g}^{-1}({f}^{-1}(a)) = g({f}^{-1}(a))](_images/math/33da1d43af869789e47738517aa4098240c72e18.png)
The tabular representation of 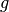 mapping is represented in hexadecimal notation as follows:
mapping is represented in hexadecimal notation as follows:
Tabular representation in hexadecimal notation
The tabular representation of 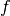 mapping is represented in hexadecimal notation as follows:
mapping is represented in hexadecimal notation as follows:
Tabular representation in hexadecimal notation
The tabular representation of 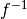 mapping is represented in hexadecimal notation as follows:
mapping is represented in hexadecimal notation as follows:
Tabular representation in hexadecimal notation
In the algorithm of Rijndael there are multiplications of a variable with a constant. A mapping called xtime is implemented in the algorithm in order to multiply by 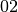 . Since all elements of
. Since all elements of 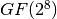 can be written as a sum of powers of
can be written as a sum of powers of 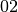 , multiplication by any constant can be implemented by a repeated use of xtime. The tabular representation of xtime mapping is represented in hexadecimal notation as follows:
, multiplication by any constant can be implemented by a repeated use of xtime. The tabular representation of xtime mapping is represented in hexadecimal notation as follows:
7.8.2. Summary¶
| S-box | NL | LD | DEG | AI | MAXAC |  |
LP | DP |
|---|---|---|---|---|---|---|---|---|
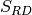 |
112 | 56 | 7 | 4 | 32 | 133120 | 0.015625 | 0.015625 |
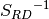 |
112 | 56 | 7 | 4 | 32 | 133120 | 0.015625 | 0.015625 |
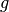 |
112 | 56 | 7 | 4 | 32 | 133120 | 0.015625 | 0.015625 |
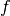 |
0 | 0 | 1 | 1 | 256 | 16777216 | 1 | 1 |
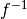 |
0 | 0 | 1 | 1 | 256 | 16777216 | 1 | 1 |
| xtime | 0 | 1 | 1 | 1 | 256 | 16777216 | 1 | 0.9921875 |
7.8.3. 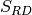 ¶
¶
7.8.3.1. Representations¶
Polynomial function over 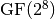 with irreducible polynomial
with irreducible polynomial 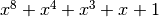 : Trace representation
: Trace representation
Polynomial representation in ANF
Walsh Spectrum representation (except first row and column):
7.8.3.2. Other useful information in cryptanalysis¶
Cycle structure:
| Cycle length | Number of cycles |
|---|---|
| 2 | 1 |
| 27 | 1 |
| 59 | 1 |
| 81 | 1 |
| 87 | 1 |
There are no linear structures
It has no fixed points. It has no negated fixed points
7.8.4. 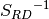 ¶
¶
7.8.4.1. Representations¶
Polynomial function over 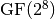 with irreducible polynomial
with irreducible polynomial 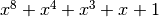 : Trace representation
: Trace representation
Polynomial representation in ANF
Walsh Spectrum representation (except first row and column):
7.8.4.2. Other useful information in cryptanalysis¶
Cycle structure:
| Cycle length | Number of cycles |
|---|---|
| 2 | 1 |
| 27 | 1 |
| 59 | 1 |
| 81 | 1 |
| 87 | 1 |
There are no linear structures
It has no fixed points. It has no negated fixed points
7.8.5.  ¶
¶
7.8.5.1. Representations¶
Polynomial representation in ANF
Walsh Spectrum representation (except first row and column):
7.8.5.2. Other useful information in cryptanalysis¶
Cycle structure:
| Cycle length | Number of cycles |
|---|---|
| 1 | 2 |
| 2 | 127 |
There are no linear structures
It has 2 fixed points: (0,0,0,0,0,0,0,0), (0,0,0,0,0,0,0,1)
It has no negated fixed points: (0,1,1,1,1,1,1,0), (1,0,0,0,0,0,0,1)
7.8.6.  ¶
¶
7.8.6.1. Representations¶
Polynomial representation in ANF
Walsh Spectrum representation (except first row and column):
7.8.6.2. Other useful information in cryptanalysis¶
Cycle structure:
| Cycle length | Number of cycles |
|---|---|
| 4 | 64 |
There are 65025 linear structures
It has no fixed points. It has no negated fixed points
7.8.7.  ¶
¶
7.8.7.1. Representations¶
Polynomial representation in ANF
Walsh Spectrum representation (except first row and column):
7.8.7.2. Other useful information in cryptanalysis¶
Cycle structure:
| Cycle length | Number of cycles |
|---|---|
| 4 | 64 |
There are 65025 linear structures
It has no fixed points. It has no negated fixed points
7.8.8. xtime¶
7.8.8.1. Representations¶
Polynomial representation in ANF
Walsh Spectrum representation (except first row and column):
7.8.8.2. Other useful information in cryptanalysis¶
Cycle structure:
| Cycle length | Number of cycles |
|---|---|
| 1 | 1 |
| 2 | 1 |
| 51 | 1 |
| 79 | 1 |
| 85 | 1 |
| 92 | 1 |
| 100 | 1 |
There are no linear structures
It has 1 fixed point: (0,0,0,0,0,0,0,0)
It has 1 negated fixed point: (0,1,0,1,0,1,0,1)
7.9. Safer+¶
7.9.1. Description¶
Safer+ (Massey et al., 1998) was submitted as a candidate for the Advanced Encryption Standard and has a block size of 128 bits. The cipher was not selected as a finalist. Bluetooth uses custom algorithms based on SAFER+ for key derivation (called E21 and E22) and authentication as message authentication codes (called E1). Encryption in Bluetooth does not use SAFER+. It has one 8x8 S-box called expf and other 9x8 S-box called logf.
7.9.2. Summary¶
| S-box | size | NL | LD | DEG | AI | MAXAC |  |
LP | DP |
|---|---|---|---|---|---|---|---|---|---|
| expf | 8x8 | 82 | 0 | 6 | 3 | 256 | 711424 | 0.1291503906 | 0.5 |
| logf | 9x8 | 164 | 0 | 6 | 3 | 512 | 4520960 | 0.1291503906 | 0.5 |
7.9.3. expf¶
7.9.3.1. Representations¶
Polynomial representation in ANF
Walsh Spectrum representation (except first row and column):
7.9.3.2. Other useful information in cryptanalysis¶
Cycle structure:
| Cycle length | Number of cycles |
|---|---|
| 1 | 3 |
| 2 | 1 |
| 41 | 1 |
| 42 | 1 |
| 168 | 1 |
There are 3 linear structures:
([1 0 0 0 0 0 0 0],[0 0 0 0 0 0 0 1])
([1 0 0 0 0 0 0 0],[0 0 0 0 0 0 1 0])
([1 0 0 0 0 0 0 0],[0 0 0 0 0 0 1 1])
It has 3 fixed points: (0,0,0,1,1,0,1,1), (0,1,0,1,0,1,1,1), (0,1,0,1,1,1,0,0)
It has 4 negated fixed points: (0,0,0,1,0,1,0,0), (0,0,1,0,1,1,0,0), (0,1,0,1,1,1,1,1), (1,0,1,0,1,1,1,1)
7.9.4. logf¶
7.9.4.1. Representations¶
Polynomial representation in ANF
Walsh Spectrum representation (first 256x256 values except first row and column):
7.9.4.2. Other useful information in cryptanalysis¶
There is 255 linear structures:
7.10. Serpent¶
7.10.1. Description¶
Serpent is a symmetric key block cipher that was a finalist in the Advanced Encryption Standard (AES) contest, where it was ranked second to Rijndael. Serpent was designed by Ross Anderson, Eli Biham, and Lars Knudsen. It has eight 4x4 S-boxes: S0, S1, S2, S3, S4, S5, S6, S7.
7.10.2. Summary¶
| S-box | NL | NL2 | LD | DEG | AI | MAXAC |  |
LP | DP |
|---|---|---|---|---|---|---|---|---|---|
| S0 | 4 | 0 | 0 | 2 | 2 | 16 | 1024 | 0.25 | 0.25 |
| S1 | 4 | 0 | 0 | 2 | 2 | 16 | 1024 | 0.25 | 0.25 |
| S2 | 4 | 0 | 0 | 2 | 2 | 16 | 1024 | 0.25 | 0.25 |
| S3 | 4 | 0 | 0 | 2 | 2 | 16 | 1024 | 0.25 | 0.25 |
| S4 | 4 | 0 | 0 | 2 | 2 | 16 | 1024 | 0.25 | 0.25 |
| S5 | 4 | 0 | 0 | 2 | 2 | 16 | 1024 | 0.25 | 0.25 |
| S6 | 4 | 0 | 0 | 2 | 2 | 16 | 1024 | 0.25 | 0.25 |
| S7 | 4 | 0 | 0 | 2 | 2 | 16 | 1024 | 0.25 | 0.25 |
7.10.3. S0¶
7.10.3.1. Representations¶
Polynomial representation in ANF
Walsh Spectrum representation (except first row and column):
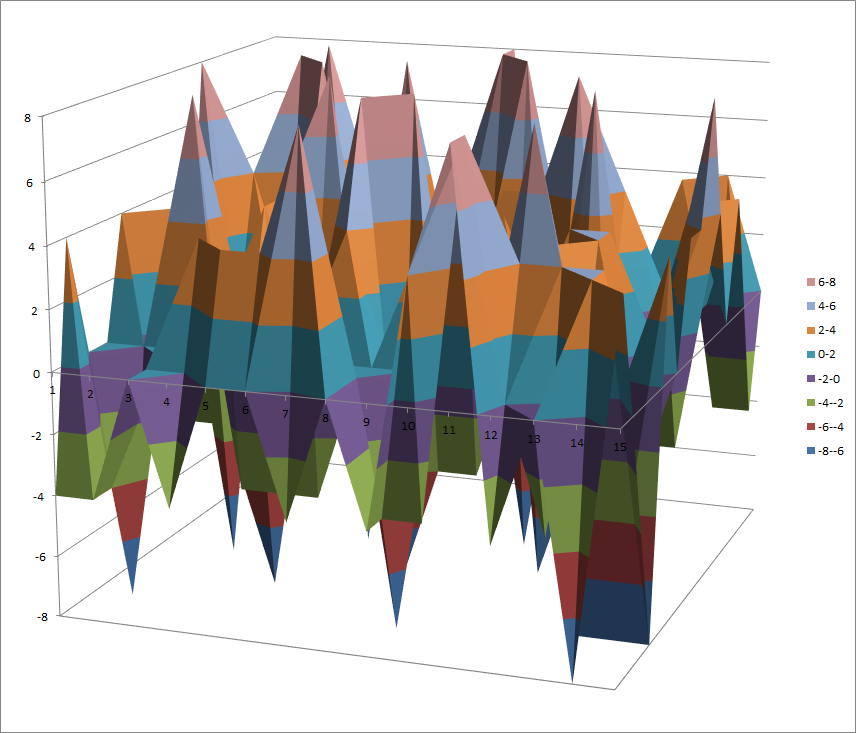
7.10.3.2. Other useful information in cryptanalysis¶
Cycle structure:
| Cycle length | Number of cycles |
|---|---|
| 2 | 2 |
| 5 | 1 |
| 7 | 1 |
There are 9 linear structures:
([0 0 1 0],[1 0 0 0])
([0 1 0 0],[0 0 1 1])
([0 1 0 0],[1 0 0 0])
([0 1 0 0],[1 0 1 1])
([0 1 1 0],[1 0 0 0])
([1 0 0 1],[0 0 1 1])
([1 0 1 1],[1 0 1 1])
([1 1 0 1],[0 0 1 1])
([1 1 1 1],[1 0 1 1])
It has no fixed points. It has no negated fixed points
7.10.4. S1¶
7.10.4.1. Representations¶
Polynomial representation in ANF
Walsh Spectrum representation (except first row and column):
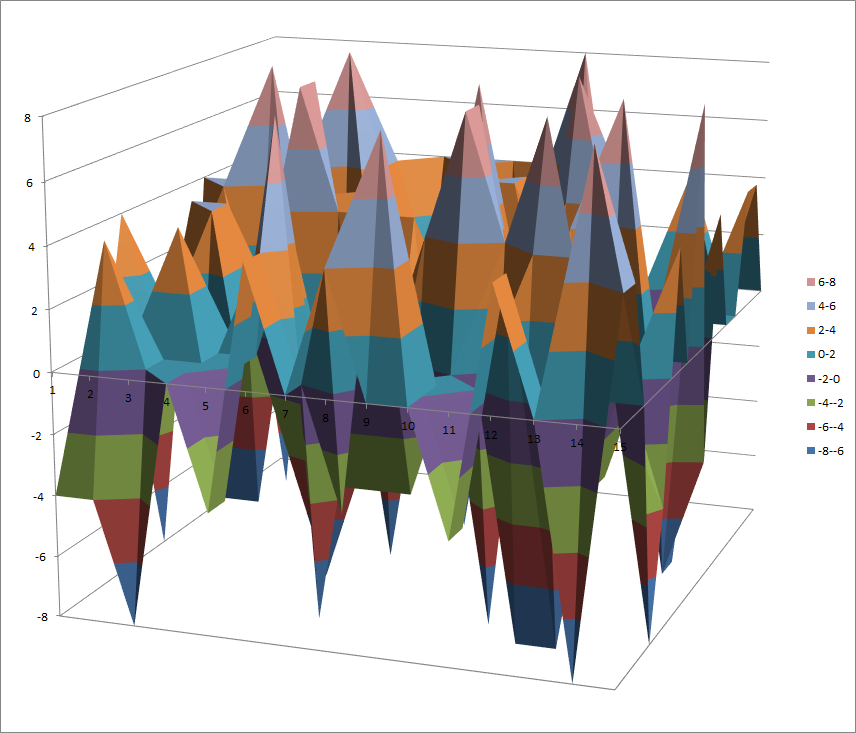
7.10.4.2. Other useful information in cryptanalysis¶
Cycle structure:
| Cycle length | Number of cycles |
|---|---|
| 1 | 2 |
| 4 | 1 |
| 10 | 1 |
There are 9 linear structures:
([0 0 1 1],[1 1 1 0])
([0 1 0 0],[0 1 0 0])
([0 1 0 0],[1 0 1 0])
([0 1 0 0],[1 1 1 0])
([0 1 1 1],[1 1 1 0])
([1 0 0 0],[0 1 0 0])
([1 0 1 1],[1 0 1 0])
([1 1 0 0],[0 1 0 0])
([1 1 1 1],[1 0 1 0])
It has 1 fixed point: (0,0,1,0)
It has 1 negated fixed point: (0,0,0,0)
7.10.5. S2¶
7.10.5.1. Representations¶
Polynomial representation in ANF
Walsh Spectrum representation (except first row and column):
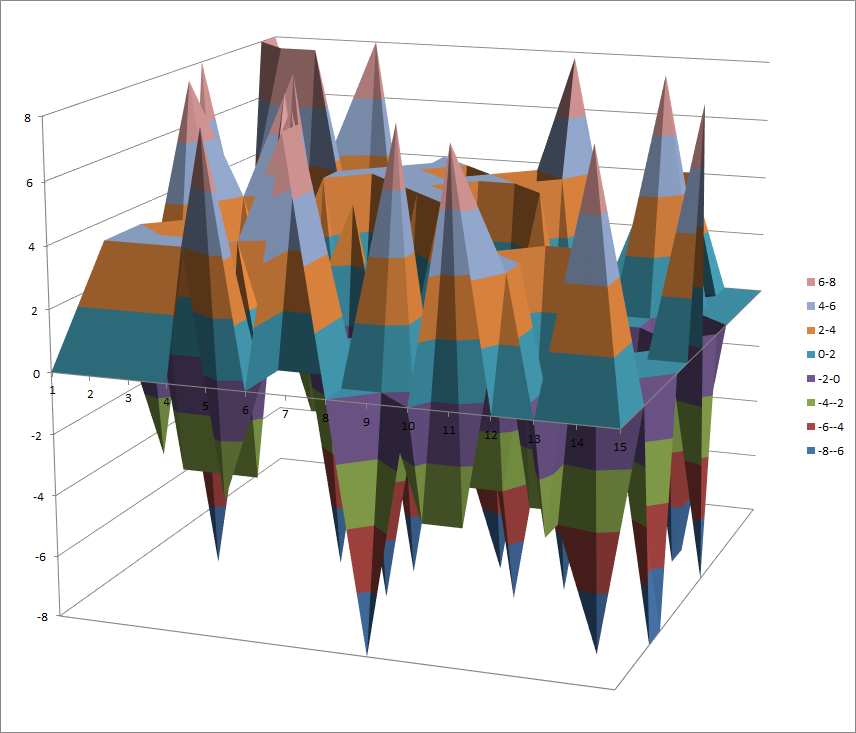
7.10.5.2. Other useful information in cryptanalysis¶
Cycle structure:
| Cycle length | Number of cycles |
|---|---|
| 3 | 1 |
| 13 | 1 |
There are 9 linear structures:
([0 0 1 0],[0 0 0 1])
([0 0 1 0],[1 1 1 0])
([0 0 1 0],[1 1 1 1])
([0 1 0 0],[1 1 1 0])
([0 1 1 0],[1 1 1 0])
([1 0 0 0],[0 0 0 1])
([1 0 1 0],[0 0 0 1])
([1 1 0 0],[1 1 1 1])
([1 1 1 0],[1 1 1 1])
It has no fixed points
It has 1 negated fixed point: (1,0,1,1)
7.10.6. S3¶
7.10.6.1. Representations¶
Polynomial representation in ANF
Walsh Spectrum representation (except first row and column):
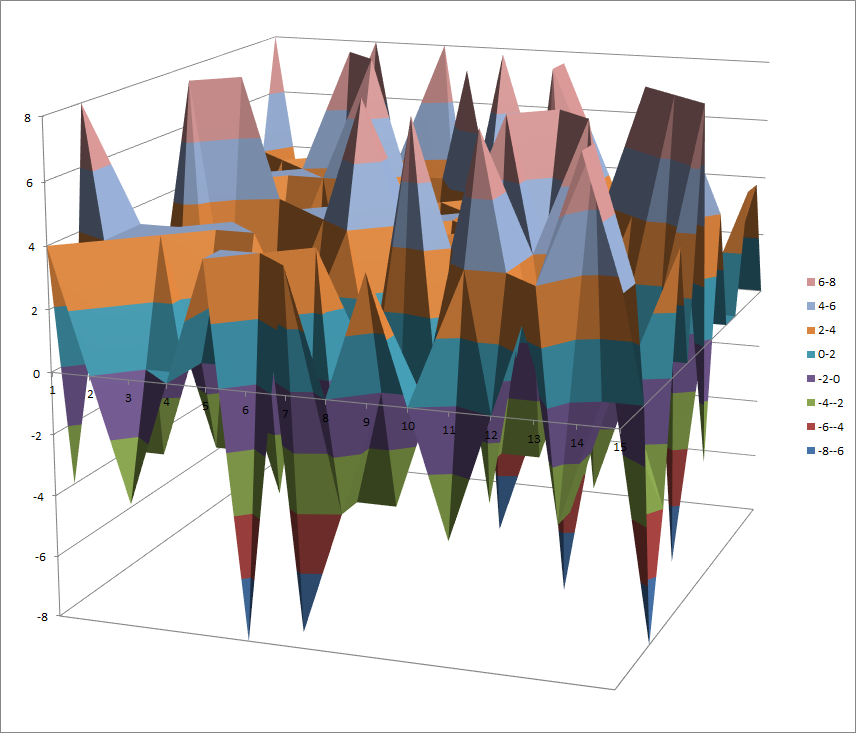
7.10.6.2. Other useful information in cryptanalysis¶
Cycle structure:
| Cycle length | Number of cycles |
|---|---|
| 1 | 2 |
| 4 | 1 |
| 5 | 2 |
There are 3 linear structures:
([0 0 1 1],[1 1 1 0])
([0 1 0 0],[1 1 1 0])
([0 1 1 1],[1 1 1 0])
It has 1 fixed point: (0,0,0,0)
It has 1 negated fixed point: (1,0,1,1)
7.10.7. S4¶
7.10.7.1. Representations¶
Polynomial representation in ANF
Walsh Spectrum representation (except first row and column):
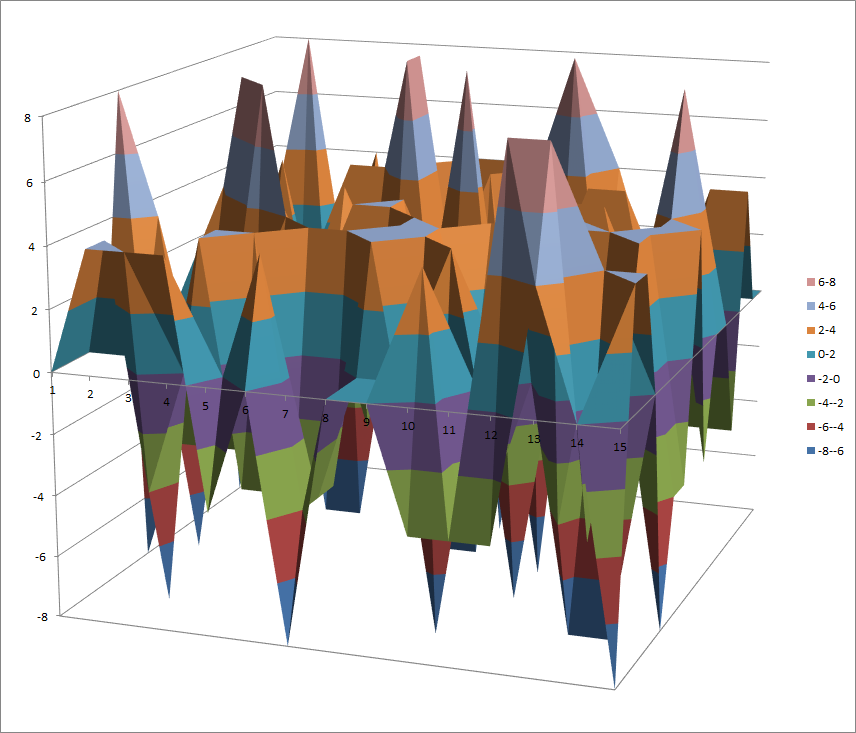
7.10.7.2. Other useful information in cryptanalysis¶
Cycle structure:
| Cycle length | Number of cycles |
|---|---|
| 1 | 1 |
| 2 | 1 |
| 13 | 1 |
There are 3 linear structures:
([0 1 0 0],[0 0 0 1])
([1 0 1 1],[0 0 0 1])
([1 1 1 1],[0 0 0 1])
It has 1 fixed point: (0,0,1,1)
It has no negated fixed points
7.10.8. S5¶
7.10.8.1. Representations¶
Polynomial representation in ANF
Walsh Spectrum representation (except first row and column):
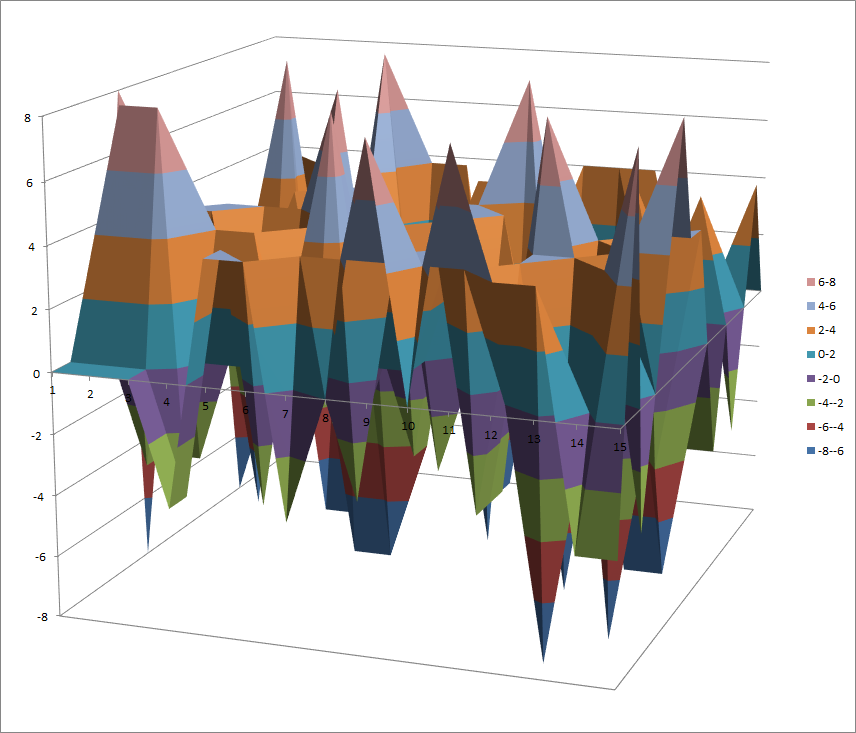
7.10.8.2. Other useful information in cryptanalysis¶
Cycle structure:
| Cycle length | Number of cycles |
|---|---|
| 1 | 2 |
| 14 | 1 |
There are 3 linear structures:
([0 1 0 0],[0 0 0 1])
([1 0 1 1],[0 0 0 1])
([1 1 1 1],[0 0 0 1])
It has 1 fixed point: (0,0,1,0)
It has 3 negated fixed points: (0,0,0,0), (0,1,0,1), (0,1,1,0)
7.10.9. S6¶
7.10.9.1. Representations¶
Polynomial representation in ANF
Walsh Spectrum representation (except first row and column):
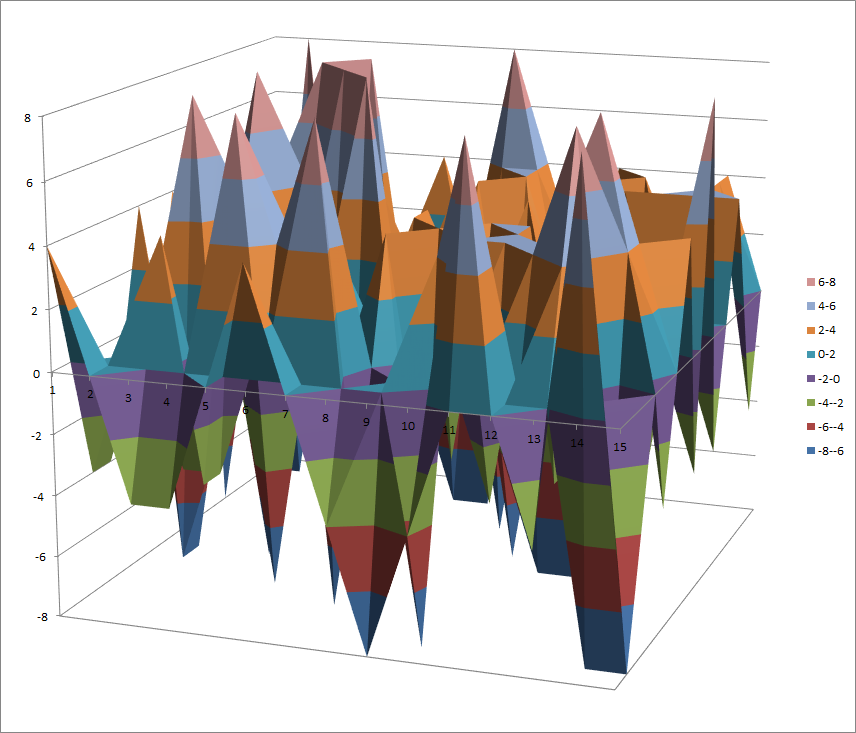
7.10.9.2. Other useful information in cryptanalysis¶
Cycle structure:
| Cycle length | Number of cycles |
|---|---|
| 1 | 2 |
| 4 | 1 |
| 10 | 1 |
There are 9 linear structures:
([0 0 1 0],[0 0 1 0])
([0 1 0 0],[0 0 1 0])
([0 1 1 0],[0 0 1 0])
([0 1 1 0],[0 1 0 1])
([0 1 1 0],[0 1 1 1])
([1 0 0 1],[0 1 0 1])
([1 0 1 1],[0 1 1 1])
([1 1 0 1],[0 1 1 1])
([1 1 1 1],[0 1 0 1])
It has 1 fixed point: (0,1,1,0)
It has 1 negated fixed point: (1,1,1,1)
7.10.10. S7¶
7.10.10.1. Representations¶
Polynomial representation in ANF
Walsh Spectrum representation (except first row and column):
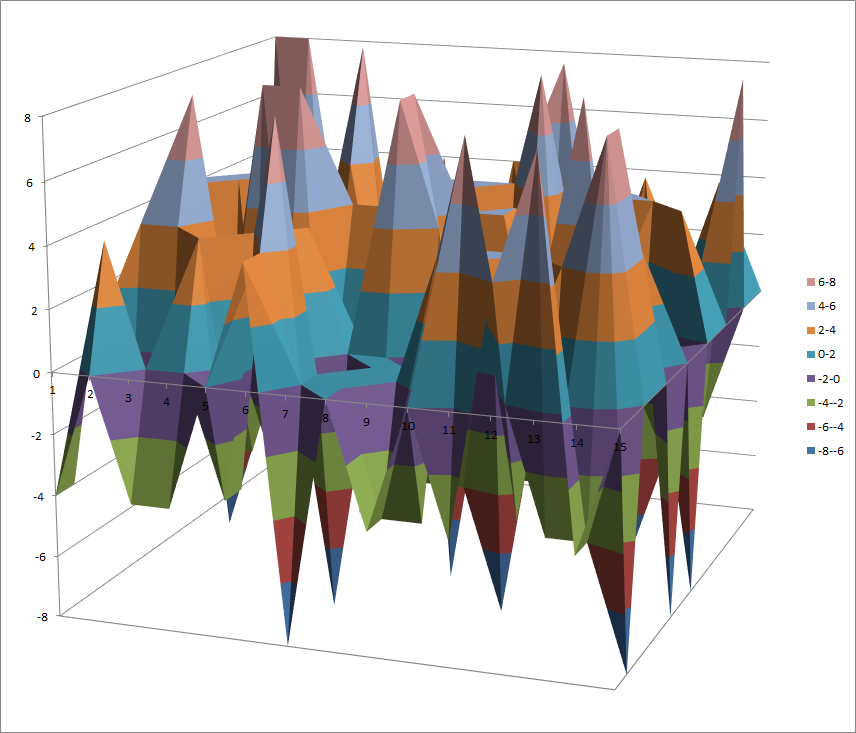
7.10.10.2. Other useful information in cryptanalysis¶
Cycle structure:
| Cycle length | Number of cycles |
|---|---|
| 3 | 1 |
| 4 | 1 |
| 9 | 1 |
There are 3 linear structures:
([0 0 0 1],[1 1 1 1])
([1 0 1 0],[1 1 1 1])
([1 0 1 1],[1 1 1 1])
It has no fixed points
It has 1 negated fixed point: (1,0,0,0)