8. Analysis of CRYPTEC project cryptographic algorithms¶
CRYPTREC is the Cryptography Research and Evaluation Committees set up by the Japanese Government to evaluate and recommend cryptographic techniques for government and industrial use. It is comparable in many respects to the European Union’s NESSIE project and to the Advanced Encryption Standard process run by NIST in the U.S.. In this chapter, certain cryptographic algorithms from CRYPTEC project candidates are analysed.
Below you can find a legend describing the cryptographic criteria used in this chapter:
| NL | Nonlinearity |
| NL2 | 2-nd order nonlinearity |
| LD | Linearity distance |
| DEG | Algebraic degree |
| AI | Algebraic immunity |
| MAXAC | Absolute indicator |
 |
Sum-of-squares indicator |
| LP | Linear potential |
| DP | Differential Potential |
Hyperlinks to representations
Open the hyperlinks to representations below in a new browser window or in a new tab.
8.1. CIPHERUNICORN-E¶
8.1.1. Description¶
CIPHERUNICORN-E is a block cipher created by NEC in 1998. It was among the cryptographic techniques recommended for Japanese government use by CRYPTREC in 2003, however, has been dropped to “candidate” by CRYPTREC revision in 2013. It has four 8x8 S-boxes: S0,S1,S2,S3
8.1.2. Summary¶
| S-box | NL | LD | DEG | AI | MAXAC |  |
LP | DP |
|---|---|---|---|---|---|---|---|---|
| S0 | 112 | 56 | 7 | 4 | 32 | 133120 | 0.015625 | 0.015625 |
| S1 | 112 | 56 | 7 | 4 | 32 | 133120 | 0.015625 | 0.015625 |
| S2 | 112 | 56 | 7 | 4 | 32 | 133120 | 0.015625 | 0.015625 |
| S3 | 112 | 56 | 7 | 4 | 32 | 133120 | 0.015625 | 0.015625 |
8.1.3. S0¶
8.1.3.1. Representations¶
Polynomial function over 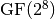 with irreducible polynomial
with irreducible polynomial 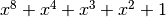 : Trace representation
: Trace representation
Polynomial representation in ANF
Walsh Spectrum representation (except first row and column):
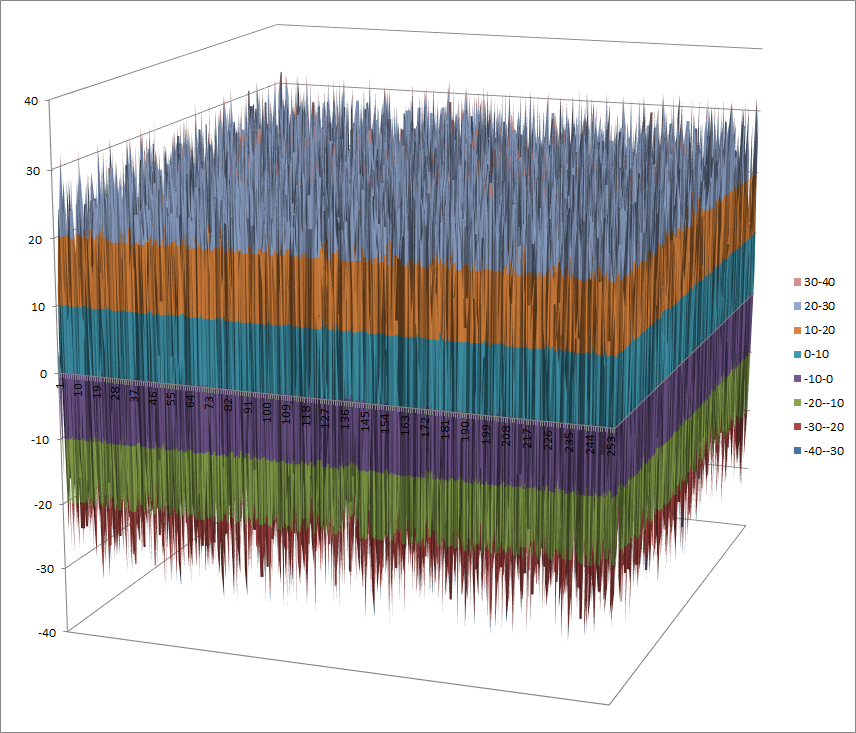
8.1.3.2. Other useful information in cryptanalysis¶
Cycle structure:
| Cycle length | Number of cycles |
|---|---|
| 2 | 1 |
| 45 | 1 |
| 209 | 1 |
There are no linear structures
It has no fixed points. It has no negated fixed points.
8.1.4. S1¶
8.1.4.1. Representations¶
Polynomial function over 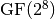 with irreducible polynomial
with irreducible polynomial 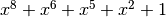 : Trace representation
: Trace representation
Polynomial representation in ANF
Walsh Spectrum representation (except first row and column):
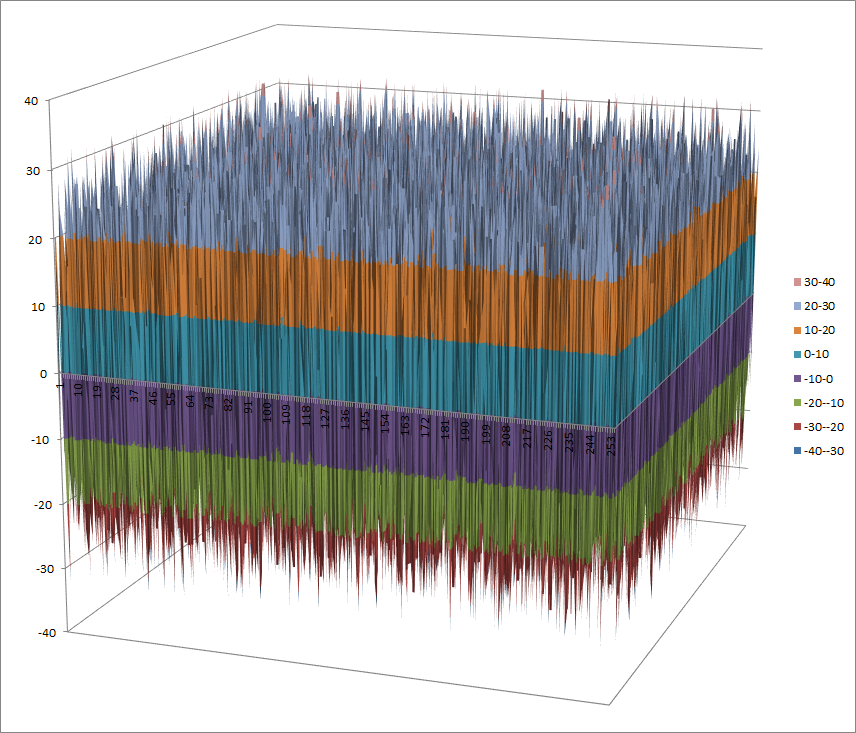
8.1.4.2. Other useful information in cryptanalysis¶
Cycle structure:
| Cycle length | Number of cycles |
|---|---|
| 2 | 1 |
| 49 | 1 |
| 205 | 1 |
There are no linear structures
It has no fixed points. It has no negated fixed points.
8.1.5. S2¶
8.1.5.1. Representations¶
Polynomial function over 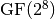 with irreducible polynomial
with irreducible polynomial 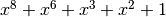 : Trace representation
: Trace representation
Polynomial representation in ANF
Walsh Spectrum representation (except first row and column):
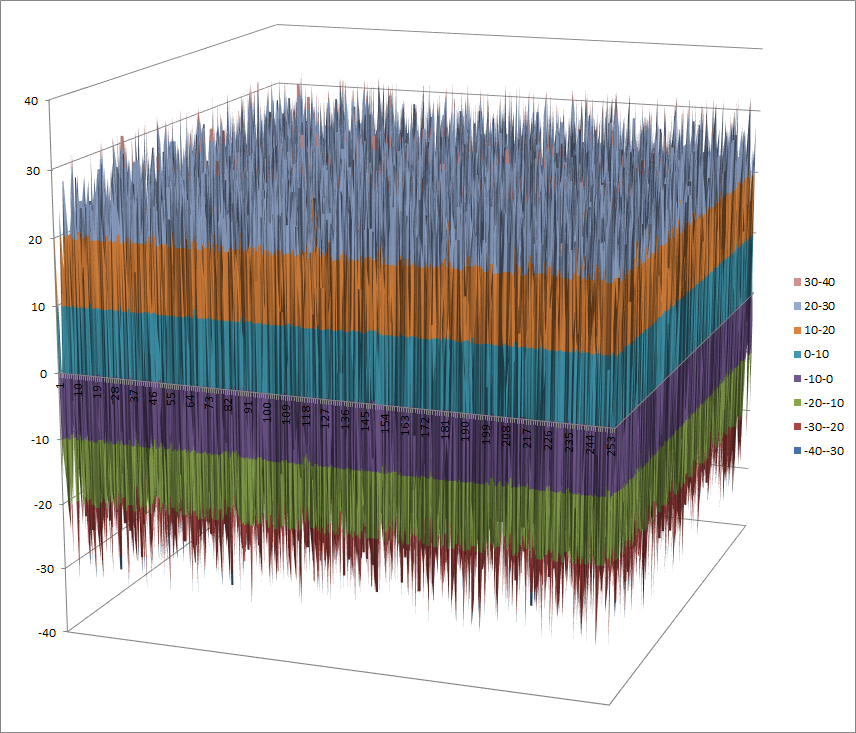
8.1.5.2. Other useful information in cryptanalysis¶
Cycle structure:
| Cycle length | Number of cycles |
|---|---|
| 4 | 1 |
| 6 | 1 |
| 33 | 1 |
| 73 | 1 |
| 140 | 1 |
There are no linear structures
It has no fixed points. It has no negated fixed points.
8.1.6. S3¶
8.1.6.1. Representations¶
Polynomial function over 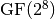 with irreducible polynomial
with irreducible polynomial 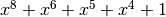 : Trace representation
: Trace representation
Polynomial representation in ANF
Walsh Spectrum representation (except first row and column):
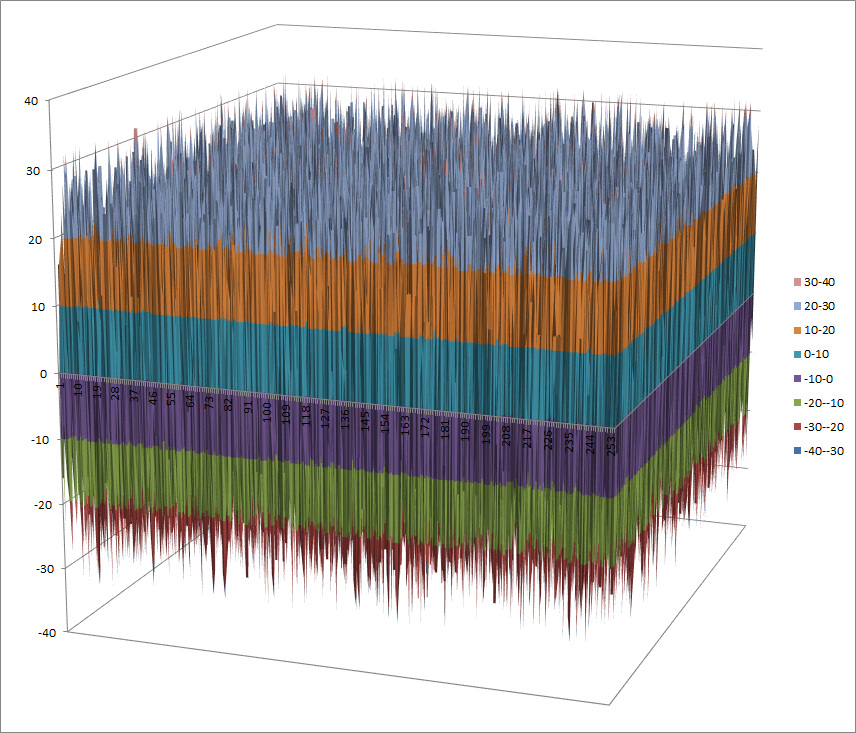
8.1.6.2. Other useful information in cryptanalysis¶
Cycle structure:
| Cycle length | Number of cycles |
|---|---|
| 3 | 2 |
| 8 | 1 |
| 21 | 1 |
| 221 | 1 |
There are no linear structures
It has no fixed points.
It has 2 negated fixed points: (0,0,1,0,0,0,1,1), (0,1,1,1,1,1,1,1)
8.2. CLEFIA¶
8.2.1. Description¶
CLEFIA is a proprietary block cipher algorithm, developed by Sony. It is intended to be used in DRM systems. It is among the cryptographic techniques recommended candidate for Japanese government use by CRYPTREC revision in 2013. It has two 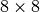 S-boxes:
S-boxes: 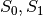
8.2.2. Summary¶
| S-box | NL | LD | DEG | AI | MAXAC |  |
LP | DP |
|---|---|---|---|---|---|---|---|---|
| S0 | 100 | 40 | 6 | 4 | 96 | 269056 | 0.0478515625 | 0.0390625 |
| S1 | 112 | 56 | 7 | 4 | 32 | 133120 | 0.015625 | 0.015625 |
8.2.3. S0¶
8.2.3.1. Representations¶
Polynomial function over 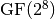 with irreducible polynomial
with irreducible polynomial 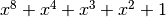 : Trace representation
: Trace representation
Polynomial representation in ANF
Walsh Spectrum representation (except first row and column):
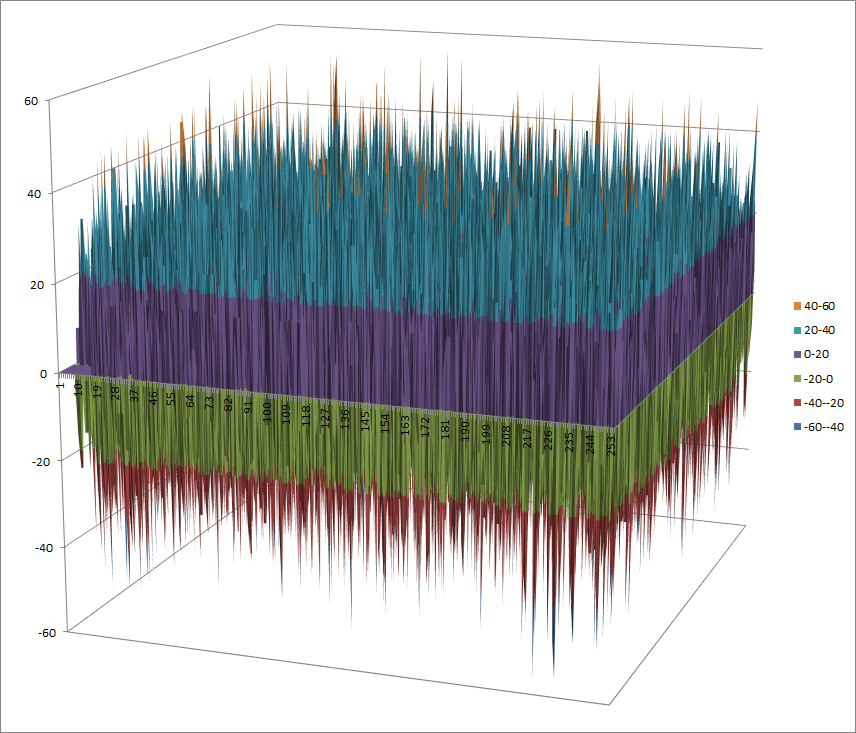
8.2.3.2. Other useful information in cryptanalysis¶
Cycle structure:
| Cycle length | Number of cycles |
|---|---|
| 4 | 1 |
| 5 | 2 |
| 17 | 1 |
| 109 | 1 |
| 116 | 1 |
There are no linear structures
It has no fixed points.
It has 2 negated fixed points: (0,1,0,0,0,0,0,1), (1,1,1,1,1,1,0,1)
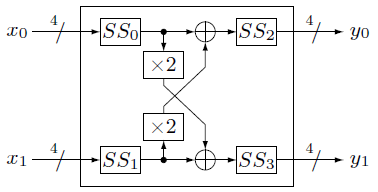
8.2.3.3. Construction¶
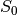 is generated by combining four 4-bit S-boxes
is generated by combining four 4-bit S-boxes 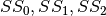 and
and 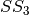 in the following way:
in the following way:
Step 1. 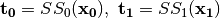 where
where 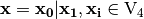
Step 2. 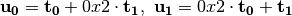
Step 3. 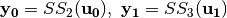 where
where 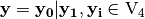
Tables of CLEFIA S-boxes 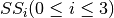 :
:
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | a | b | c | d | e | f |
| SS0(x) | e | 6 | c | a | 8 | 7 | 2 | f | b | 1 | 4 | 0 | 5 | 9 | d | 3 |
| SS1(x) | 6 | 4 | 0 | d | 2 | b | a | 3 | 9 | c | e | f | 8 | 7 | 5 | 1 |
| SS2(x) | b | 8 | 5 | e | a | 6 | 4 | c | f | 7 | 2 | 3 | 1 | 0 | d | 9 |
| SS3(x) | a | 2 | 6 | d | 3 | 4 | 5 | e | 0 | 7 | 8 | 9 | b | f | c | 1 |
The multiplication in 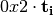 is performed in
is performed in 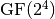 defined by the lexicographically first primitive polynomial
defined by the lexicographically first primitive polynomial 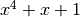 . Here we provide the table of multiplication of
. Here we provide the table of multiplication of 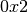 with an element modulo
with an element modulo 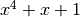 . The entries in the Table are represented in hexadecimal notation for compactness. The column indices represent the element to be multplied by
. The entries in the Table are represented in hexadecimal notation for compactness. The column indices represent the element to be multplied by 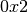 modulo
modulo 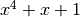 , and the product is the corresponding entry in the column.
, and the product is the corresponding entry in the column.
Table of the multiplication 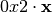 :
:
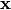 |
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | a | b | c | d | e | f |
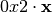 |
0 | 2 | 4 | 6 | 8 | a | c | e | 3 | 1 | 7 | 5 | b | 9 | f | d |
Next figure shows the construction of 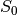 :
:
Hence, CLEFIA S0 can be denoted by:
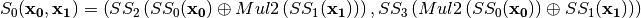
Note that the symbol  refers to the composition of functions,
refers to the composition of functions,  refers to the direct sum of functions and
refers to the direct sum of functions and 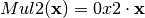 .
.
The criteria of several constructions in 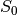 are summarized in the following tables:
are summarized in the following tables:
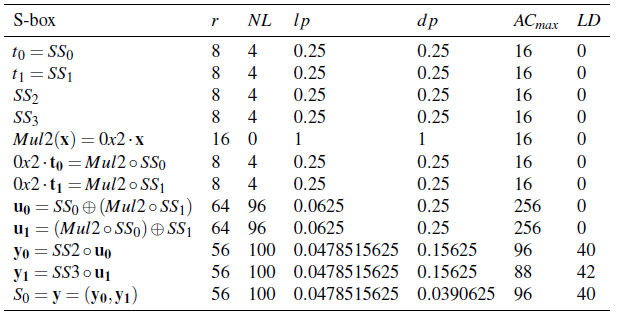
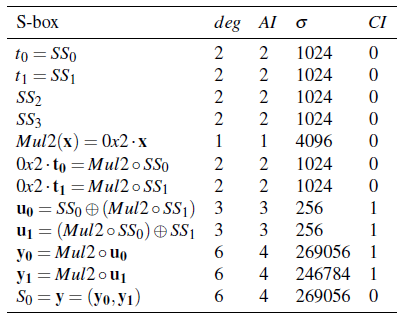
You can find a program which calculates the Truth Tables of these constructions in chapter “Operations and constructions over Vector Boolean Functions”, section “Addition of coordinate functions”.
8.2.3.3.1. Mul2¶
Let 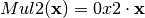 the multiplication in
the multiplication in 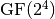 defined by the primitive polynomial
defined by the primitive polynomial 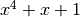 as in CLEFIA cipher.
as in CLEFIA cipher.
Polynomial representation in ANF
Cycle structure:
| Cycle length | Number of cycles |
|---|---|
| 1 | 1 |
| 15 | 1 |
There are 225 linear structures
It has 1 fixed point: (0,0,0,0)
It has 1 negated fixed point: (0,1,0,1)
8.2.3.3.2. 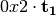 ¶
¶
The operation 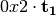 in Step 2 can be interpreted as the composition of
in Step 2 can be interpreted as the composition of 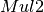 and
and 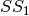 .
.
Polynomial representation in ANF
Cycle structure:
| Cycle length | Number of cycles |
|---|---|
| 1 | 2 |
| 2 | 2 |
| 10 | 1 |
There are 3 linear structures:
([0 0 1 0],[0 1 0 1])
([0 1 0 0],[0 1 0 1])
([0 1 1 0],[0 1 0 1])
It has 2 fixed points: (0,1,0,0), (0,1,0,1)
It has 1 negated fixed point: (1,1,0,0)
8.2.3.3.3. 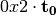 ¶
¶
The operation 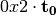 in Step 2 can be interpreted as the composition of
in Step 2 can be interpreted as the composition of 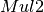 and
and 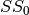 .
.
Polynomial representation in ANF
Cycle structure:
| Cycle length | Number of cycles |
|---|---|
| 16 | 1 |
There are 3 linear structures:
([0 0 1 1],[1 0 0 1])
([1 0 0 1],[1 0 0 1])
([1 0 1 0],[1 0 0 1])
It has no fixed points.
It has 1 negated fixed point: (0,0,0,0)
8.2.3.3.4. 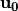 ¶
¶
The operation 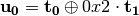 in Step 2 can be interpreted as the direct sum of
in Step 2 can be interpreted as the direct sum of 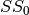 and
and 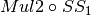 .
.
Polynomial representation in ANF
There are 6 linear structures:
([0 0 0 0 0 0 1 0],[0 1 0 1])
([0 0 0 0 0 1 0 0],[0 1 0 1])
([0 0 0 0 0 1 1 0],[0 1 0 1])
([0 0 1 1 0 0 0 0],[1 1 0 0])
([1 0 0 1 0 0 0 0],[1 1 0 0])
([1 0 1 0 0 0 0 0],[1 1 0 0])
8.2.3.3.5. 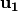 ¶
¶
The operation 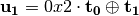 in Step 2 can be interpreted as the direct sum of
in Step 2 can be interpreted as the direct sum of 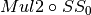 and
and 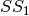 .
.
Polynomial representation in ANF
There are 6 linear structures:
([0 0 0 0 0 0 1 0],[1 0 1 0])
([0 0 0 0 0 1 0 0],[1 0 1 0])
([0 0 0 0 0 1 1 0],[1 0 1 0])
([0 0 1 1 0 0 0 0],[1 0 0 1])
([1 0 0 1 0 0 0 0],[1 0 0 1])
([1 0 1 0 0 0 0 0],[1 0 0 1])
8.2.3.3.6. 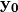 ¶
¶
In the Step 3, 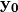 is obtained by composing
is obtained by composing 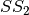 S-box with
S-box with 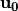 .
.
Polynomial representation in ANF
There are no linear structures.
8.2.3.3.7. 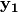 ¶
¶
In the Step 3, 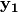 is obtained by composing
is obtained by composing 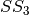 S-box with
S-box with 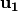 .
.
Polynomial representation in ANF
There are no linear structures.
8.2.4. S1¶
8.2.4.1. Representations¶
Polynomial function over 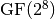 with irreducible polynomial
with irreducible polynomial 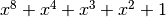 : Trace representation
: Trace representation
Polynomial representation in ANF
Walsh Spectrum representation (except first row and column):
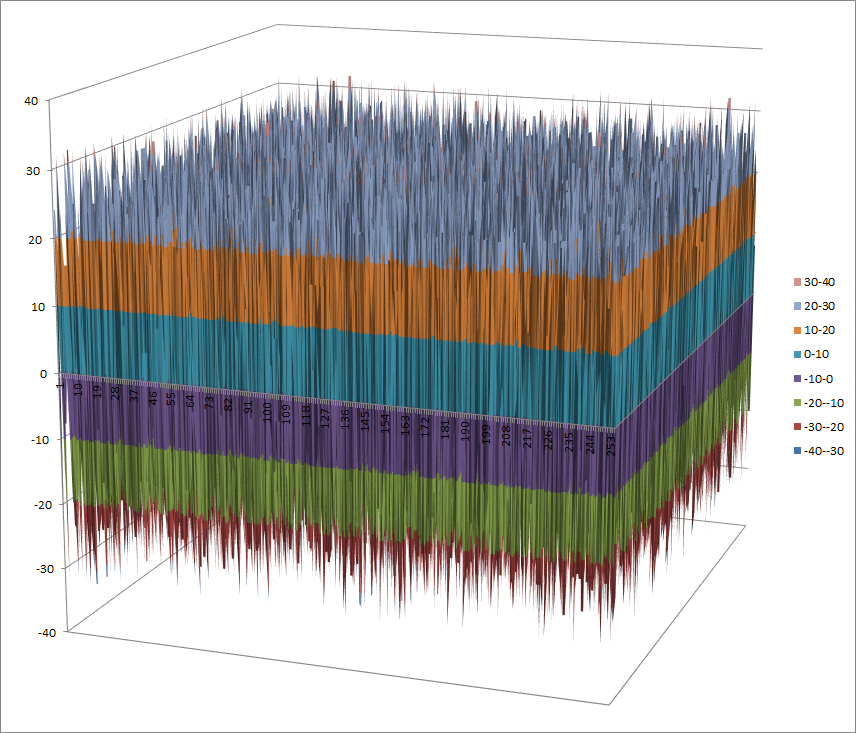
8.2.4.2. Other useful information in cryptanalysis¶
Cycle structure:
| Cycle length | Number of cycles |
|---|---|
| 256 | 1 |
There are no linear structures
It has no fixed points.
It has 1 negated fixed point: (0,0,1,1,1,0,1,0)
8.3. Hierocrypt3¶
8.3.1. Description¶
Hierocrypt3 and Hierocrypt-L1 are block ciphers created by Toshiba in 2000. They were submitted to the NESSIE project, but were not selected. Both algorithms were among the cryptographic techniques recommended for Japanese government use by CRYPTREC in 2003, however, both have been dropped to “candidate” by CRYPTREC revision in 2013. Both of them have the same 8x8 S-box: S
8.3.2. Summary¶
| S-box | NL | LD | DEG | AI | MAXAC |  |
LP | DP |
|---|---|---|---|---|---|---|---|---|
| S | 112 | 56v | 7 | 4 | 32 | 133120 | 0.015625 | 0.015625 |
8.3.3. S¶
8.3.3.1. Representations¶
Polynomial function over 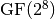 with irreducible polynomial
with irreducible polynomial 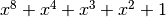 : Trace representation
: Trace representation
Polynomial representation in ANF
Walsh Spectrum representation (except first row and column):
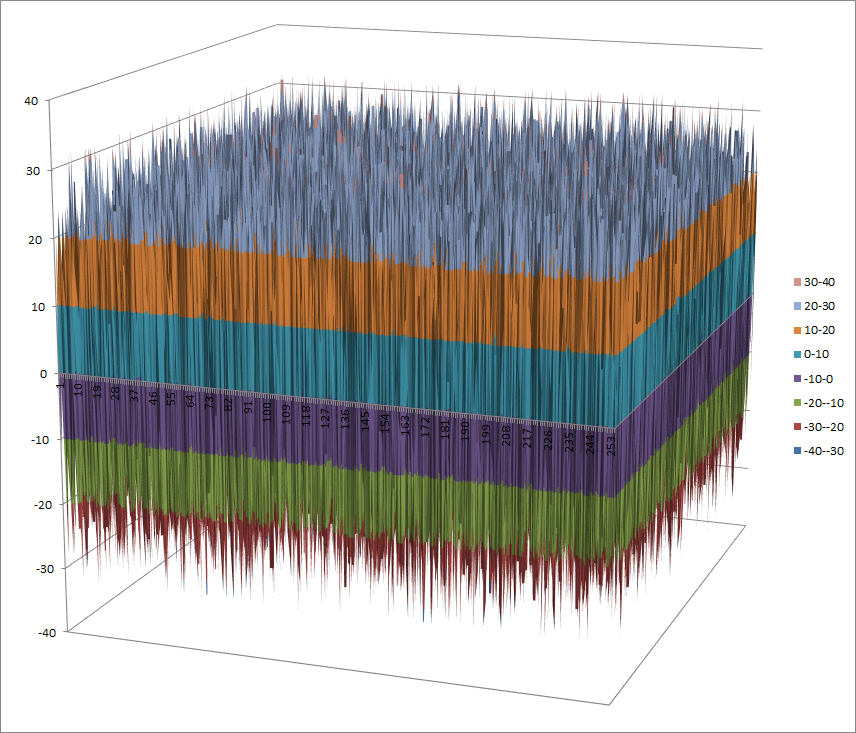
8.3.3.2. Other useful information in cryptanalysis¶
Cycle structure:
| Cycle length | Number of cycles |
|---|---|
| 1 | 1 |
| 2 | 1 |
| 3 | 1 |
| 109 | 1 |
| 141 | 1 |
There are no linear structures
It has 1 fixed point: (0,1,1,0,0,1,1,1)
It has 2 negated fixed points: (0,0,0,1,0,1,1,1), (1,0,0,1,0,1,0,0)
8.4. SC2000¶
8.4.1. Description¶
SC2000 is a block cipher invented by a research group at Fujitsu Labs. It was submitted to the NESSIE project, but was not selected. It was among the cryptographic techniques recommended for Japanese government use by CRYPTREC in 2003, however, has been dropped to “candidate” by CRYPTREC revision in 2013. It has three 3 S-boxes: S4,S5,S6
8.4.2. Summary¶
| S-box | size | NL | NL2 | LD | DEG | AI | MAXAC |  |
LP | DP |
|---|---|---|---|---|---|---|---|---|---|---|
| S4 | 4x4 | 4 | 0 | 0 | 2 | 2 | 16 | 1024 | 0.25 | 0.25 |
| S5 | 5x5 | 12 | 6 | 6 | 3 | 3 | 8 | 2048 | 0.0625 | 0.0625 |
| S6 | 6x6 | 24 | 14 | 12 | 5 | 3 | 16 | 8704 | 0.0625 | 0.0625 |
8.4.3. S4¶
8.4.3.1. Representations¶
Polynomial representation in ANF
Walsh Spectrum representation (except first row and column):
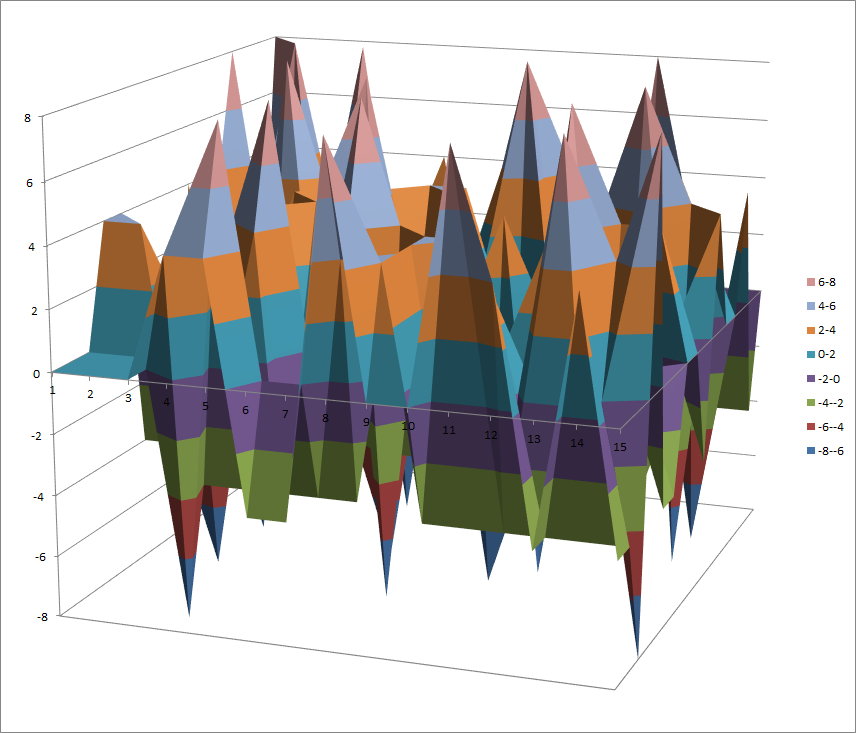
8.4.3.2. Other useful information in cryptanalysis¶
Cycle structure:
| Cycle length | Number of cycles |
|---|---|
| 2 | 1 |
| 3 | 1 |
| 11 | 1 |
There are 3 linear structures:
([0 1 0 1],[0 0 1 1])
([1 0 0 1],[0 0 1 1])
([1 1 0 0],[0 0 1 1])
It has no fixed points.
It has 2 negated fixed points: (0,0,1,1), (1,0,0,1)
8.4.4. S5¶
8.4.4.1. Representations¶
Polynomial representation in ANF
Walsh Spectrum representation (except first row and column):
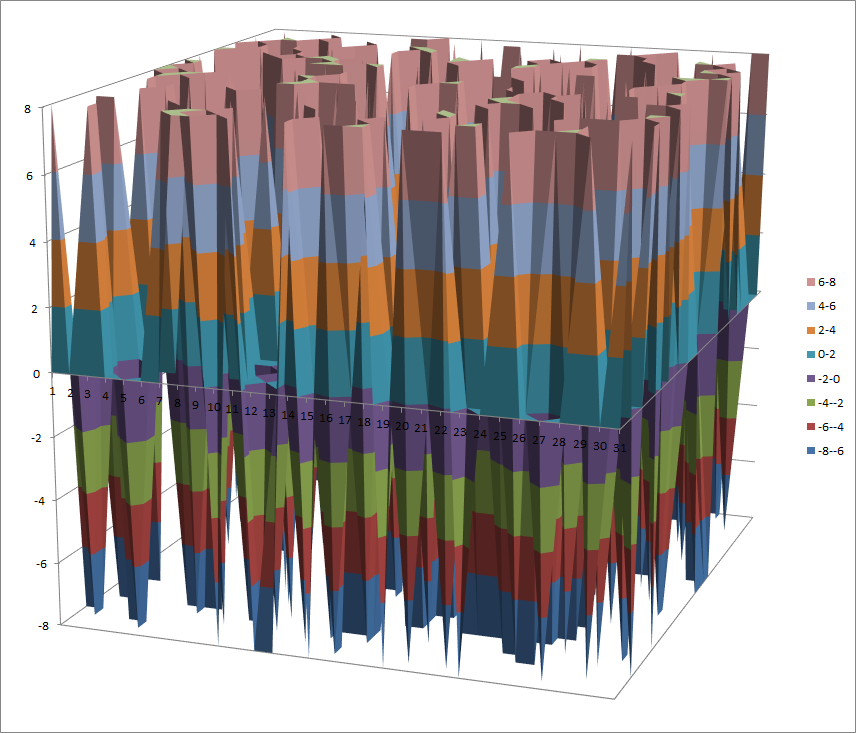
8.4.4.2. Other useful information in cryptanalysis¶
Cycle structure:
| Cycle length | Number of cycles |
|---|---|
| 6 | 1 |
| 8 | 2 |
| 10 | 1 |
There are no linear structures
It has no fixed points. It has no negated fixed points
8.4.5. S6¶
8.4.5.1. Representations¶
Polynomial representation in ANF
Walsh Spectrum representation (except first row and column):
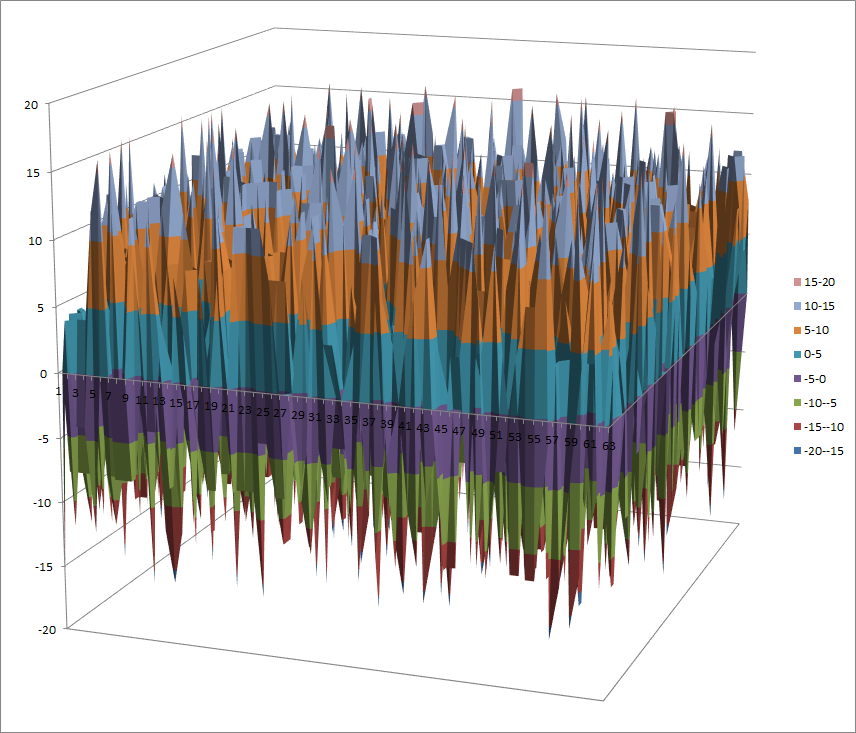
8.4.5.2. Other useful information in cryptanalysis¶
Cycle structure:
| Cycle length | Number of cycles |
|---|---|
| 2 | 2 |
| 9 | 1 |
| 17 | 1 |
| 34 | 1 |
There are no linear structures
It has no fixed points. It has no negated fixed points